2022. 10. 11. 15:18ㆍ수학,과학,공학
내 아이가 볼 만한
2010-12-23 00:27:44

미분과 적분의 개념을 발명한 사람은 일반적으로 영국의 뉴턴이나 독일의 라이프니츠라고 알려져 있다. 두 사람 중 누가 미적분학을 먼저 만들었느냐, 혹은 두 사람이 독자적으로 거의 동시에 미적분학을 만들었느냐로 치열한 공로 다툼이 있다는 것은 알만한 사람은 안다. 하지만 이 두 사람에 앞서 근대 미적분학을 만드는 데 중요한 역할을 한 선구자가 더 있었다는 건 그다지 많이 알려져 있지 않는데, 오늘 수학 산책에서는 그 중의 한 명인 피에르 드 페르마(Pierre de Fermat, 1601-1665)를 만나보자.
아주 오랜 법칙 : 빛의 반사

접선을 구하는 문제가 가장 자연스럽게 등장하는 분야라면 광학이 으뜸이다. 곡선이나 곡면 등에 빛을 쏘았을 때 반사되어 나가는 빛의 방향을 구하는 것이 광학의 기본인데, 이는 바로 접선 및 접평면을 구하는 문제로 이해할 수 있기 때문이다. 평면 거울에 빛을 발사한 경우 어느 방향으로 빛이 반사되는지는 대부분 알 것이다. 빛이 휘는 경우를 생각지 않으면, 직선에 빛을 쏜 경우만 생각해도 충분하다. 쏜 빛이 반사되어 나가는 방향은 흔히 ‘입사각과 반사각이 같다’는 단순한 원리로 알아낼 수 있다. 직선이 아니라 곡선에 빛을 쏠 경우에는, 빛이 부딪히는 점에서의 접선에 빛을 쏘았다고 간주하고 반사된 방향을 구하면 된다.

포물면의 원리(좌)와 이를 이용한 안테나(우)
예를 들어 y축과 나란하게 들어온 빛이 포물선 y=kx2 에 부딪혀 반사된 빛은 초점 (0, k/4)에 모인다는 것을 접선을 써서 증명할 수 있다. 물론 이 사실 자체는 접선이나, 미분에 대해서는 몰랐던 고대인들도 이미 알고 있었는데, 아르키메데스가 이런 원리를 이용하여 무기를 만들었다는 전설까지 있다. 현대에도 조명등, 등대, 망원경, 렌즈, 안테나 등을 제작할 때 포물면의 원리를 사용하는 경우가 많은데, 좀더 복잡한 용도에 쓰는 광학 도구를 제작하려면 접선과 미분의 개념을 아는 것이 유용하다.
빛의 굴절 법칙
그런데 빛은 반사만 하는 게 아니라, 굴절도 한다. 굴절률이 다른 매질이 맞닿아 있을 때, 이를 통과하는 빛이 경계면에서 꺾이는 현상 역시 오래 전부터 관찰한 사실로, 서기 140년에 프톨레미는 실험 결과를 표로 작성하기도 했다. 이 표로부터 일반적인 법칙을 처음 제시한 사람은 스넬(Willebrord Snell, 1580-1620)이니, 참으로 오랜 세월이 걸렸다. 흔히 ‘스넬의 법칙’으로 부르는 법칙으로, 아래 그림에 나타낸 입사각 θi및 굴절각 θr에 대해 다음 식이 성립한다는 것이다.

여기서 n은 두 매질에 의해 결정되는 상수다.

스넬의 법칙을 설명하는 그림(좌), 굴절률이 높은 매질에서 낮은 매질로 빛이 진행할 때는 입사각이 어떤 임계각을 넘으면 전반사가 일어난다(우)
스넬의 법칙에서 n이 1보다 작은 경우가 특히 흥미롭다. 편의상 n=2/3이라고 해보자. 입사각이 커서 sinθi 가 2/3을 넘어가는 경우 스넬 법칙 때문에 sinθr는 1보다 커야 하므로 불가능한 일이 벌어진다. 물리적으로는 굴절이 일어날 수 없다는 것으로 해석할 수 있다. 따라서 경계면에 도달한 빛은 꺾여서 밖으로 빠져나가지 않고, 원래 매질 속으로 고스란히 반사되어 되돌아간다. 이런 현상을 전반사(total reflection, 全反射)라고 한다. 광섬유를 통해 손실을 줄이고 정보를 보낼 수 있는 것도 이런 원리를 활용하고 있다. 잘 만든 법칙 하나가 얼마나 세상을 바꿀 수 있는지 알 수 있다.
페르마의 임계점 정리
물리 산책인지 수학 산책인지 혼란을 야기하기 전에 서둘러 페르마를 소환하기로 하자. 페르마는 자신은 증명하지도 못한 마지막 정리로 너무나도 유명한 나머지, 정작 수론, 확률론, 광학 등에서 남긴 업적이 가려지는 경우가 많다. 웬만한 전문 수학자를 능가했던 아마추어 수학자 페르마가 광학을 연구하면서 미분의 초기 개념을 일군 사실도 그다지 알려져 있지 않다. 잠시 옆길로 새서 극점이라는 개념부터 도입하기로 하자. 함수 y=f(x)가 x=a에서 극소라는 것은 x=a 근방에서는 f(a)가 최솟값일 때를 말하고, 극대라는 것은 x=a 근방에서 f(a)가 최댓값일 때를 말한다. 이 둘을 뭉뚱그려서 극점이라 부른다. 페르마는 ‘극점 근방에서는 함숫값의 변화가 거의 없다’고 했다. 이를 ‘임계점 정리’라 부르는데, 현대적인 표현으로 쓰면 다음과 같다.
y = f(x) 가 x=a에서 극점을 가지면, 다음 둘 중의 하나다.
1. x=a에서 미분이 불가능하거나
2. f’(a) = 0이다.
미분이 가능할 경우, f’(a) > 0 이면 기울기가 양수인 직선과 비슷할 테니 증가할 것이고, 반대로 f’(a) < 0 이면 감소할 테니 x=a가 극점일 수 없다는 건 그럴듯해 보인다. ‘비슷해 보인다’는 표현을 쓸 때는 주의해야 하는데 직관과 어긋나는 경우가 있기 때문이다. 이런 애매한 표현을 피해 수학적으로도 엄밀하게 대여섯 줄이면 증명할 수 있는데, 일생에 한 번은 증명해 보는 것도 좋겠다. 어쨌거나 접선을 구하기 위해 발명됐던 미분이 무궁무진에 가까운 응용력을 갖게 된 데는 별 것 아니게 보이는 (이 말 자주 하는 것 같다) 임계점 정리의 공이 컸다. 관심 있어 하는 함수가 최대나 최소를 가질 경우 최댓값이나 최솟값을 구하는 것은 기본일 텐데, 최대인 곳에서는 당연히 극대이고, 최소인 곳에서는 당연히 극소이기 때문에 임계점 정리를 쓸 수 있다. 바로 임계점 정리 덕에 미분이 함수의 최대와 최소를 구하는 강력한 무기로 부상할 수 있었던 것이다. 미분은 더는 접선을 구하는 도구로 만족하지 않는 것이다.
페르마의 최소 시간의 원리

임계점 정리의 응용은 무수히 많다. 경제 문제, 물리 문제, 수학 문제 등에서 언제 최대인지, 언제 최소인지, 언제 평형 상태에 이르는지 등의 질문만 나오면 임계점 정리가 고개를 내민다. 다 소개할 수도 없거니와, 여기서는 페르마가 광학에 어떻게 응용하여 굴절 법칙을 설명했는지 소개하는 게 흐름에도 맞는 것 같다.

| A를 출발하여 굴절된 빛이 B에 도달할 때, 빛이 취하는 경로는 ‘최단 거리 경로’가 아니다. 최단 거리 경로라면 A, B를 잇는 직선 경로를 따라야 하기 때문이다. 그렇다면 빛이 취하는 경로는 어떤 경로일까? 페르마는 ‘최소 시간의 원리’를 제안하여 이 문제를 해결한다. 즉, A에서 B에 도달할 때 빛이 취하는 경로는 ‘시간이 가장 적게 드는 경로’여야 한다는 얘기다. 일단 이 원리를 받아들일 경우, 어떻게 스넬의 법칙을 유도할 수 있는지 알아보자. 오른쪽 그림에서처럼 경계면으로부터의 점 A의 높이를 a라 하고, 점 B의 깊이를 b라 하자. 또한 AB의 수평 거리를 c라 하자. 경계면에 닿기 전까지 빛의 속도를 v, 경계면을 지나친 후의 빛의 속도를 w라 하자. A로부터 수평거리 x인 곳에서 굴절이 됐다면, A에서 B까지 이르는 데 걸린 시간은 다음과 같다. |

미분법을 배운 이들은 임계점 정리를 써서 다음과 같은 경우에 시간이 최소임을 쉽게 알 수 있을 것이다.

한편 위 그림을 생각해보면, sin θi 와 sin θr은 아래와 같다.

및
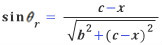
따라서, n=v/w라 두어 스넬의 법칙을 얻을 수 있다. 상수 n의 정체까지 덤으로 알 수 있다! 물론 페르마는 오늘날과 같은 형태의 미분을 알지는 못했으므로, 조금은 다른 방식으로 설명했다. 지면 관계상 생략하지만 페르마가 설명한 방식은 라그랑지의 ‘최소 작용의 원리’ 등으로 이어져 수리 물리학에 많은 영향을 끼쳤다. 수학에서도 아예 ‘변분법’(calculus of variation)이라는 분야가 만들어지기도 했다.
어렵기도 하고, 재미 있기도 한 최소 시간의 원리
최소 시간의 원리가 유용한 것은 반사 법칙까지 한꺼번에 설명할 수 있기 때문이다. 최소 시간의 원리를 정확히 이해하려면 빛의 파동성을 이해해야 하고, 양자 역학을 알아야 한다고 한다. 고전 역학의 범위 내에서는 최소 작용의 원리 정도로 충분한 편인데, 물리산책에서 한번쯤 다뤄줬으면 하는 소망이 있다.
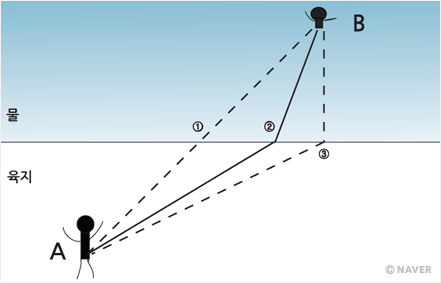
A위치의 사람이 B의 위치에 물에 빠진 사람을 구하려면 ①,②,③ 중 어느 경로로 가야 가장 빠를까?
보통 사람은 수영 속도가 뛰는 속도보다 느리므로 ②의 경로로 가야 한다.
글 정경훈 / 서울대 기초교육원 강의교수 서울대학교 수학과에서 학사, 석사, 박사를 받고, 포항공대, 연세대, 위스콘신대, 서울대에서 박사후 과정을 밟았다. 현재 서울대 기초교육원 강의교수이다.
'수학,과학,공학' 카테고리의 다른 글
| 671-방사선의-정체 (0) | 2022.10.11 |
|---|---|
| 658. 영국엔 천재가 많은듯 (0) | 2022.10.11 |
| 638. 아날렘마 (0) | 2022.10.11 |
| 528. 비만에 대한 오해와 진실 (0) | 2022.10.11 |
| 519-가슴-안열고-심장-구멍-메우고-위-안자르고-癌세포만-벗겨내 (1) | 2022.10.11 |