758. 이를 계산해보면 18,446,744,073,709,551,615 번

2015-04-23 10:17:43

---

하노이의 탑. 3개의 막대에 원판을 규칙에 따라 옮기는 퍼즐. <출처: gettyimageskorea>

아마도 꽤 많은 사람들이 ‘재귀’라는 단어를 한번쯤 들어보았을 것이다. 중, 고등학교 영어시간 때 재귀대명사에 대해 배운 적이 있을테니까. 기억을 돌이켜보면 재귀 대명사는 주어의 동작이 다시 주어로 되돌아가는 관계를 나타내는 대명사라 배웠을 것이다.

이와 같이 자기 자신이 다시 반복되는 예는 우리 실생활에서도 찾아볼 수 있다. 높은 산에 올라가서 ‘야호’를 외치거나 동굴 속에서 이야기를 할 때 우리가 말한 말이 여러 번 반복해서 들리게 된다. 또한 거울이 사방에 설치된 엘리베이터 안에서 거울을 볼 때 거울 속 자신의 모습이 계속해서 반복적으로 나타나는 것을 본 적이 있을 것이다. 우리가 알아볼 재귀 알고리즘도 이들과 같은 원리이다. 재귀 알고리즘이란 무엇이고 어떠한 과정을 거치는지 알아보자.

거울이 사방에 설치된 엘리베이터에서 안에서 거울을 보면 자신의 모습이 계속해서 반복적으로 나타난다. 이런 것을 응용한 것이 재귀 알고리즘이다. <출처: gettyimageskorea>

 

어떠한 문제를 자기 자신을 호출하여 해결하는 과정

재귀(Recursion) 알고리즘이란 어떠한 문제를 자기 자신을 호출하여 해결하는 과정을 말한다. 정의만 보면 아직 이해하기 어려울 수 있지만, 이 알고리즘은 매우 효과적으로 쓰일 수 있다. 재귀 알고리즘이 어떠한 방식으로 이루어지는지 알아보자. 먼저 아래에 나열된 수를 보자. 아래의 수들은 일정한 규칙으로 계속 진행된다. 그렇다면 10번째 수는 무엇이 될까?

이 문제는 재귀 알고리즘으로 쉽게 해결할 수 있다. 먼저 위의 수들에 적용되는 규칙이 무엇인지 알아야한다. 위의 수들을 자세히 살펴보면 다음과 같은 규칙을 알아낼 수 있다.

위의 규칙을 보면 3번째 수는 2번째 수에 3을 더한 값이고, 6번째 수는 5번째 수에 6을 더한 값이 된다. 따라서 n번째 수는 n-1번째 수에 n을 더한 값이라는 것을 알 수 있다. 먼저 S(n)을 n번째 수라고 가정해보자. 그렇다면 S(n-1)은 n-1번째 수가 된다. 재귀 알고리즘은 자기 자신을 활용하는 것이므로 S(n)을 S(n-1)로 정의할 수 있어야 한다. 따라서 위의 규칙을 다음과 같은 식으로 일반화 할 수 있다.

이제 위의 식을 이용해 다음처럼 하나씩 대입해가면서 10번째 수를 구할 수 있다.

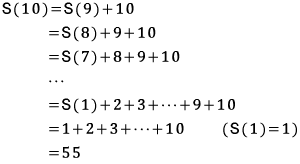
지금까지 재귀 알고리즘에 대해 간단히 살펴보았다. 이제 이러한 재귀의 힘을 가장 잘 보여주는 예인 하노이 탑 문제에 대해 소개를 하려고한다. 여러분은 한번쯤은 하노이 탑에 대해 들어보았을 것이다. 먼저 하노이 탑의 유래는 다음과 같다.

 

‘하노이의 탑’ 문제

인도 베나레스에 있는 한 사원에는 세상의 중심을 나타내는 큰 돔이 있고 그 안에 세 개의 다이아몬드 바늘이 동판 위에 세워져 있습니다. 바늘의 높이는 1 큐빗이고 굵기는 벌의 몸통만 합니다. 바늘 가운데 하나에는 신이 64개의 순금 원판을 끼워 놓았습니다. 가장 큰 원판이 바닥에 놓여 있고, 나머지 원판들이 점점 작아지며 꼭대기까지 쌓아 있습니다. 이것은 신성한 브라흐마의 탑입니다. 브라흐마의 지시에 따라 승려들은 모든 원판을 다른 바늘로 옮기기 위해 밤낮 없이 차례로 제단에 올라 ‘규칙’에 따라 원판을 하나씩 옮깁니다. 이 일이 끝날 때, 탑은 무너지고 세상은 종말을 맞이하게 됩니다.

< 출처: 위키백과 - 하노이의 탑>

위의 이야기에 나오는 전설1)의 탑을 하노이 탑이라고 부른다. 그렇다면 원판 64개를 다른 막대로 옮기는데 최소로 드는 횟수는 얼마가 될까? 먼저 위 이야기에 나온 ‘규칙’을 정리하면 다음과 같다.

1. 맨 위의 원판만 옮겨야 한다.
2. 한 번에 하나의 원판만 옮겨야 한다.
3. 작은 원판 위에 큰 원판이 올라갈 수 없다.

원판의 개수가 64개로 너무 많기 때문에 어떤 식으로 풀어야 할지 감이 안 잡힌다. 먼저 이 문제를 해결하기 전에 원판이 3개라면 어떤 과정을 거치는지부터 생각해보자. 모든 원판들을 막대 A에서 C로 옮기는 과정을 그림으로 나타내면 다음과 같다.

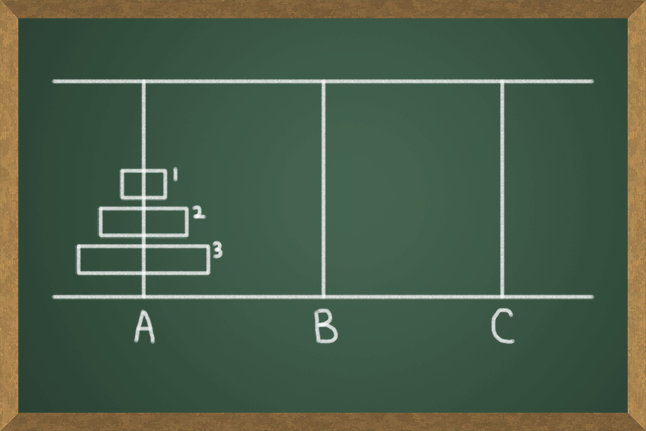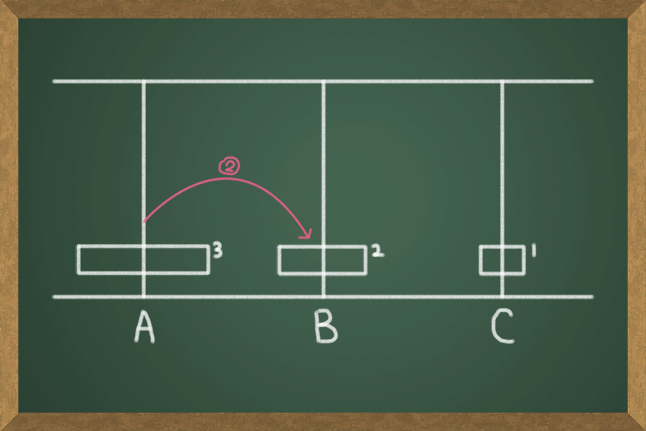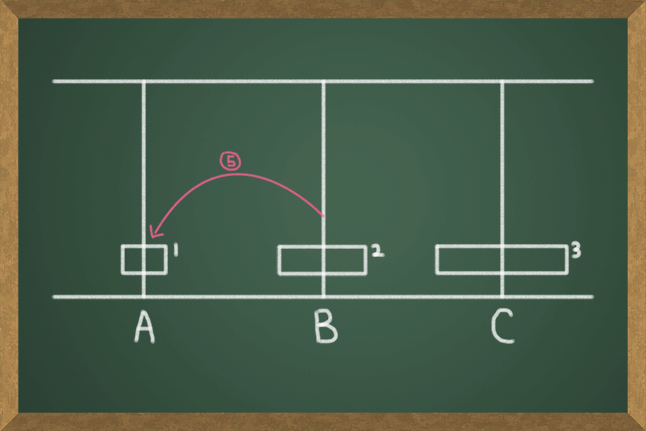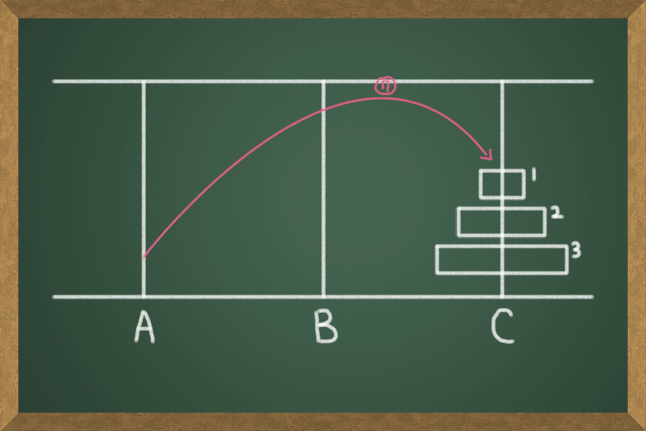
위의 과정을 통해 원판 3개를 옮기는데 드는 횟수는 7번이라는 것을 알 수 있다. 원판의 개수가 3개밖에 안되기 때문에 그림으로 차근차근 그려가면서 쉽게 해결할 수 있다. 하지만 원판의 수가 많아지면 하나하나 다 그릴 수 없고 그리더라도 너무 복잡해진다. 원판의 개수가 20개, 64개, 그 이상일 경우는 어떻게 해결해야 할까?

 

재귀 알고리즘의 힘

위의 과정을 조금 다르게 생각해보자. 먼저 바로 가장 아래에 있는 원판을 C로 옮기고 싶지만 위에 있는 원판 2개 때문에 그럴 수 없다. 따라서 위의 원판 2개를 B로 옮겨야 가장 아래의 원판을 C로 옮길 수 있게 된다. 이는 가장 아래에 있는 원판을 옮기려면 그 위에 있는 원판들을 먼저 다른 곳으로 옮겨야한다는 뜻이다. 즉, 원판 3개를 옮기기 위해서는 먼저 원판 2개를 옮기는 방법부터 생각해봐야한다. 이런 식으로 생각을 확장하면, 원판 7개를 옮기려면 먼저 원판 6개를 옮기는 방법을 생각해야하고, 원판이 20개라면 원판 19개를 옮기는 방법부터 생각해야 한다는 것을 알 수 있다. 이제 다음 과정을 살펴보자. 다음은 원판이 4개일 경우를 3단계로 거쳐서 설명한 것이다.

원판이 4개일 경우도 마찬가지로 가장 아래에 있는 원판(4)을 C로 옮겨야 한다. 하지만 위에 있는 원판(1), 원판(2), 원판(3) 때문에 그럴 수 없다. 따라서 먼저 원판(1), 원판(2), 원판(3)을 다음 그림처럼 B로 옮겨야 한다. 우리는 바로 앞에서 원판 3개를 C로 옮기는 방법에 대해 배웠다. 원판 3개를 C로 옮기나 B로 옮기나 드는 횟수는 똑같지 않겠는가? 따라서 위에 있는 원판 3개를 B로 옮기는 데 드는 횟수는 7번이라는 사실을 알 수 있다. 다음 과정을 보자.

이제 막대 A에 있는 가장 큰 원판(4) 위에 아무 것도 없어졌다. 이제 원판(4)을 C로 옮기면 된다. 이는 딱 한 번의 횟수가 든다.

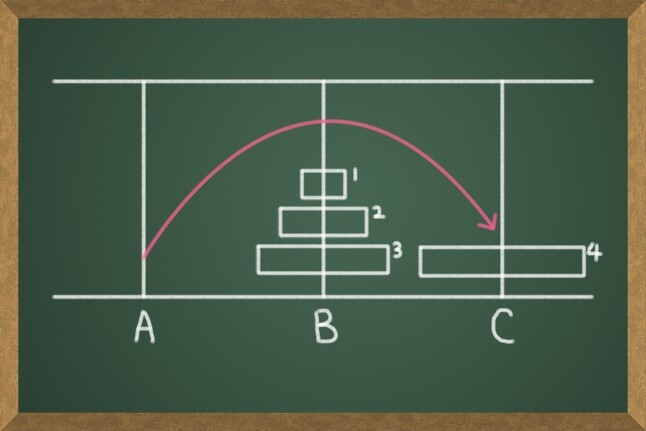
가장 큰 원판(4)이 막대 C의 가장 아래로 갔기 때문에 B에 있는 나머지 원판 3개를 원판(4) 위로 옮기면 된다. 이도 역시 원판이 3개기 때문에 7번의 횟수가 든다는 것을 알 수 있다.

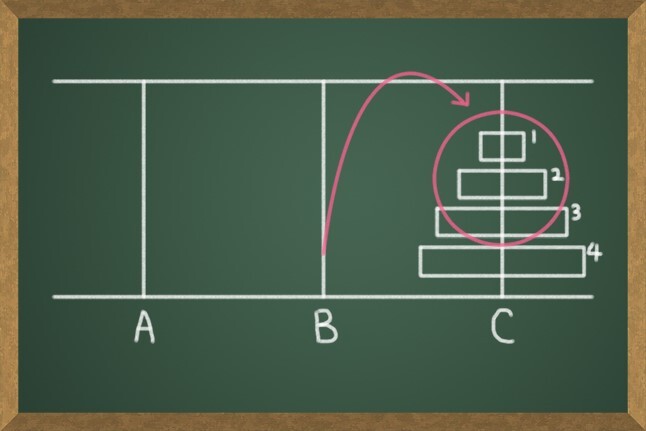
이렇게 원판 4개를 A에서 C로 옮기는 과정을 3단계로 나눠보았다. 총 횟수를 세어보면 다음과 같이 15번이 된다.

1. 위에 있는 원판 3개를 B로 옮긴다 : 7번
2. 가장 아래에 있는 원판을 C로 옮긴다 : 1번
3. B에 있는 원판 3개를 다시 C로 옮긴다 : 7번

이제 원판이 n개일 경우를 생각해보자. 먼저 함수를 다음과 같이 정의해보자.

원판 n개를 옮기는 경우도 마찬가지로 먼저 위에 있는 원판 n-1개를 옮겨야 한다. 따라서 옮기는 과정은 다음과 같다. 위의 원판 4개를 옮기는 과정에서 숫자만 바꾼 셈이다.

1. 위에 있는 원판 

개를 B로 옮긴다 : 

번
2. 가장 아래에 있는 원판을 C로 옮긴다 : 1번
3. ’B'에 있는 원판 

개를 다시 C로 옮긴다 : 

번

따라서 모두 더하면 다음과 같은 식을 얻을 수 있다.

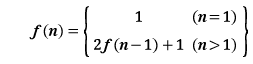
이제 위 식을 이용하여 원판이 64개일 경우일 때 드는 횟수를 계산해보자. 이전에 10번째 수를 구한 것처럼 하나씩 대입해가면서 구할 수 있다. 하지만 일일이 다 적어가며 구하기에는 시간이 오래 걸리게 되므로, f(n)이 어떻게 되는지 알아보자.

f(n)은 f(n-1)에 2를 곱하는 과정이 있으니, 2의 거듭제곱과 관계가 있다는 것을 짐작할 수 있다. 그리고, f(n)값의 처음 몇 개를 구해보면 아래와 같다.

2의 거듭 제곱은 2, 4, 8, 16, 32, 64 …의 순이니 f(n)은 아래와 같다는 것을 알 수 있다. 실제로 식에 대입해보면 이 결과가 옳다는 것을 쉽게 확인할 수 있다.

이제 우리는 원판이 64개를 옮기는데 드는 횟수를 쉽게 구할 수 있다. n에 64를 대입하면, 264-1번만큼 옮겨야 한다. 이를 계산해보면 18,446,744,073,709,551,615번이라 한다. 이 어마어마한 숫자를 재귀 알고리즘을 이용하면 쉽게 구할 수 있다. 그런데, 원판을 1초에 한번을 옮긴다고 하면, 쉬지 않고 원판을 옮긴다고 하더라도 이만큼 옮기는데 걸리는 시간은 5814억년이 넘게 걸린다고 한다. 전설에 따르자면 세상의 종말은 꽤 많이 남은 셈이다.

 

재귀 알고리즘를 여러 문제 해결에 응용된다

지금까지 하노이 탑 문제를 재귀 알고리즘을 이용해 해결해보았다. 많은 복잡한 알고리즘들을 재귀를 이용해 쉽고 효과적으로 해결할 수 있다. 하노이 탑 말고도 피보나치 수열, 팩토리얼 함수 계산, 이진 탐색 등 재귀를 이용해 해결할 수 있는 알고리즘들이 많이 있다. 이러한 문제들을 위에서 다루었던 재귀 알고리즘을 이용해 해결해보길 바란다.

피보나치 수열
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55

팩토리얼 함수

이렇게 반복이 필요한 알고리즘을 구현하는 데 재귀 알고리즘 외에 반복(Iteration) 알고리즘이 있다. 반복 알고리즘이란 for문이나 while문 등의 반복문을 이용해 어떠한 조건을 만족할 때까지 일정 부분을 계속 반복시키는 형태이다. 이는 함수를 다시 호출하는 방법이 아닌, 단순한 반복이기 때문에 수행속도 면에서는 재귀 알고리즘보다 앞설 수 있지만, 그에 비해 코딩이 복잡해지거나 가독성에 어려움이 있는 단점이 있을 수 있다.

---

 부록: 하노이의 탑 문제 재귀 알고리즘의 슈도 코드

다음은 하노이 탑 문제를 해결하기 위해 사용된 재귀 알고리즘을 슈도코드로 간략히 나타낸 것이다. 아래의 코드가 쉽게 와 닿지 않을 수 있지만 몇 줄 안 되기 때문에 천천히 읽어보면 이해할 수 있을 것이다.

줄코드

1	Recursion Algorithm
2
3	f(n)
4	{
5	if(n==1) // n이 1이라면,
6	return 1 // 1의 값을 반환한다.
7
8	return 2×f(n-1)+1 // n이 1이 아니면, 2×f(n-1)+1의 값을 반환한다.
9	}

위의 코드를 보면 f(n0안에 자기 자신인 f(n-1)을 호출하고 있다는 것을 알 수 있다. 이런 식으로 일정 부분의 알고리즘이 계속 반복되는 것이다. 따라서 재귀 알고리즘에서 중요한 점은 재귀로 인해 계속 반복되는 점을 멈추는 부분이 필요하다는 것이다. 그렇지 않다면 알고리즘은 무한히 반복되고 결국 에러를 발생시키게 된다.

다음은 위의 f(n0에서 n에 3을 대입한, f(3)의 과정을 나타낸 것이다.

글안성진 | 성균관대학교 컴퓨터교육과 교수성균관 대학교 정보공학과를 졸업하고 동 대학원에서 박사학위를 받았다. 한국컴퓨터교육학회 회장, 미래창조과학부 ICT인재양성전문위원회 위원장 등을 역임했고, 행정안전부장관표창, 대통령표창을 받았다. 현재 성균관대학교 컴퓨터교육과 교수이다. [Naver 소프트웨어야 놀자] 캠페인에 자문을 하고 있다.인물정보 더보기

글고근호 | 성균관대학교 컴퓨터교육과 재학