2022. 10. 13. 11:00ㆍ수학,과학,공학
2014-08-09 01:34:35
|
2012/01/24 16:05 http://blog.naver.com/oscarsim_95/60153721639 |
설날 전날에 수학공식이나 쓰고 있는 나란 남자.
하지만 설날 마지막에 마무리 하는 나란 남자.
우선 오일러의 공식이란?
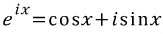
입니다.
보통 세타로 표현하기도 하지만, 일단 공식이니만큼 x로 표현하겠습니다.
절대 제가 일일이 그리스문자 넣기 귀찮아서 그런게 아닙니다.
수학에서는 '완벽한 공식' 등등으로 평해지기도 하는데,
우선 그 완벽이 무엇이냐 하면, x에 파이를 대입해보면
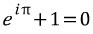
이라는 등식이 성립합니다.
우리가 고등학교 들어서 가장 많이 쓰는 자연상수 e, 허수 i,원주율 파이, 숫자 0과 1이 모두 포함되있죠.
뭐 여러모로 간단해보이지만, 허수승이라는게 어떻게 나올수 있는지도 궁금합니다.
증명 방법은 미적분, 수열의 극한 등 여러가지가 알려져있습니다만,
저는 복소수의 극형식으로 증명하겠습니다.
우선 복소평면부터 설명해야겠군요.
복소평면은 일반 직교좌표계와 별로 다를 것은 없지만,
x축이 실수, y축이 허수를 나타냅니다.
간단하게 복소수
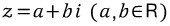
(단 a,b는 실수)
형식으로 나타낸다고 하면 이 복소수는
직교좌표계에서 (a,b)에 대응됩니다.
실수값만큼 오른쪽, 허수 i 의 계수만큼 위쪽으로 가는거죠. 물론 음수면 반대.
복소수의 극형식을 말하기 전에, 혹시 극좌표계를 아시나요?
우리가 흔히 쓰는 직교좌표계 (x,y)와 달리,
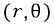
로 나타내어지며, r은 반지름, 세타는 x축의 양의 방향과의 동경을 나타냅니다.
예를 들어 (1,1)이 있다면 거리는 루트2이고, 각도는 45도이니
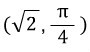
가 되는거죠.
이와 비슷한 형식으로, 복소수의 좌표 (a,b)를
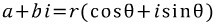
로 나타낼 수 있습니다.
이것이 복소수의 극형식입니다.
왜냐 하면,
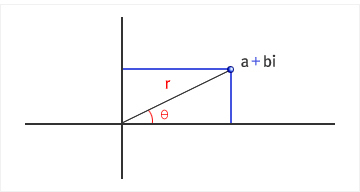
<네이버캐스트 펌>
로 보이듯이, 빗변길이 r 각도 세타의 직각삼각형을 생각하시면 됩니다.
가로길이는 r코사인, 세로길이는 r사인이 되겠죠.
그런데 왜 대체 난데없이
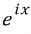
가 등장하는걸까요?
이것에 대해서는 테일러 급수에 대하여 알아야 합니다.
http://blog.naver.com/oscarsim_95/60142910176 (테일러 급수에 대하여)
에서 테일러 급수에 대해 잠깐만 읽고오시면 됩니다. 아시는 분은 패스.
바로 전 포스팅입니다.
보셨다면
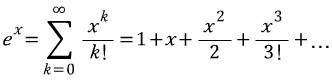
인 것을 알 수 있습니다.
아무리 미분해도 그대로죠.
그렇다면 이 x 대신, ix를 살짝 대입해줍시다.
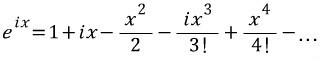
조금 복잡해졌군요.
그럼 허수부를 i로 묶어 실수부와 구분해보겠습니다.
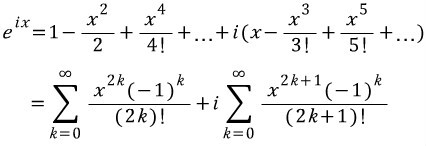
자, 이 식은 어떻게 정리해야 할까요?
http://blog.naver.com/oscarsim_95/60142910176
이전 포스팅을 읽으셨다면 알겠지만,
실수부는 코사인함수의 테일러급수, 허수부는 사인함수의 테일러급수입니다.
그렇다면
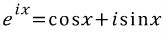
가 성립하게 되는 것입니다.
증명 완료.
*************보너스************
이 유용한 공식은 여러 군데에 쓰일수 있습니다.
예를 들면,
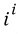
같은 터무니없는, 허수인지 실수인지조차 짐작가지 않는 수를 구할 수 있습니다.
구하는 방법은 간단합니다.
i가 들어가지 않은 코사인항을 없애기 위해
x에 2분의 파이를 대입해줍시다.
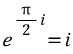
이제 양변을 i승 해줍시다.
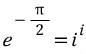
즉, 실수의 실수승이므로 실수가 나오게 됩니다. 우와아..
값은 대략 0.208 이라는듯 하군요. 물론 무리수
문제점 있으면 댓글로.
'수학,과학,공학' 카테고리의 다른 글
| 726-불같은-사랑이-오래가지-못하는-이유 (0) | 2022.10.13 |
|---|---|
| 724. 자주 멍 때리기 (0) | 2022.10.13 |
| 720. 현대 암호는 푸는 게 불가능 한 게 아니라 (0) | 2022.10.13 |
| 716. 노력하면 된다? 글쎄.. (0) | 2022.10.13 |
| 715. 인류가 차지하는 공간 (0) | 2022.10.13 |