2022. 10. 13. 11:06ㆍ수학,과학,공학
내 아이가 볼 만한
2014-08-13 08:01:07

물리학의 수많은 법칙들 가운데 보통 사람들에게 비교적 친숙한 법칙이 에너지 보존 법칙이다. 에너지 보존 법칙이란 외력이 작용하지 않는 어떤 고립된 물리계(system)의 에너지는 그 형태가 달라질 수는 있으나 그 총량은 항상 보존된다는 법칙이다. 즉 고립된 계의 에너지는 새로이 생겨나거나 혹은 사라지지 않는다.
고립된 물리계의 에너지 총량은 항상 보존된다 : 에너지 보존 법칙

역학적 에너지의 보존은 놀이동산의 롤러코스터에서도 볼 수 있다.
에너지란 일을 할 수 있는 능력을 일컫는다. 여기서 일(work)이란 물리적으로 정의된 양으로 어떤 물체에 힘이 작용하여 그 방향으로 물체가 움직였을 때, 그 이동거리와 힘의 곱으로 주어진다. 쉽게 말해 에너지란 힘을 들여 뭔가를 움직일 수 있는 능력을 말한다. 에너지에는 여러 종류가 있다. 운동에너지, 화학에너지, 퍼텐셜에너지, 열에너지, 소리에너지, 빛에너지, 전기에너지 등등. 고립된 계의 에너지는 그 총량이 보존되는 한도 안에서 모든 가능한 형태로 바뀔 수 있다.
갈릴레이가 생각했던 빗면 실험을 떠올려 보자. 빗면 위에 구슬을 가만히 놓아두면 처음에는 이 구슬이 중력에 대한 퍼텐셜에너지만 가진다. 처음에는 정지해 있으므로 운동에너지는 없다. 이제 구슬이 빗면을 굴러 내려오면 퍼텐셜에너지는 줄어들고 운동에너지는 그만큼 늘어난다. 만약 구슬이 빗면을 다 내려와 지면에 닿게 되면 구슬의 퍼텐셜에너지는 없어진다. 대신 구슬은 그만큼의 운동에너지를 가지고 지면을 따라 굴러간다. 즉 구슬의 퍼텐셜에너지가 운동에너지로 바뀐 것이다. 만약 지면에 마찰이 없으면 구슬은 한없이 굴러갈 것이다. 왜냐하면 고립된 계의 에너지는 보존되기 때문이다.
에너지 보존 법칙은 열역학 제 1법칙 이기도 하다
하지만 현실에서는 이런 일이 일어나지 않는다. 마찰 때문이다. 마찰이 있으면 열이나 소리로 에너지가 새어 나간다. 에너지 보존을 생각할 때는 열이나 소리처럼 가능한 모든 형태의 에너지를 고려해야 한다. 에너지 보존 법칙이 열역학 제1법칙인 이유가 바로 여기에 있다. 열은 에너지의 한 형태이다. 주전자에 물을 넣고 팔팔 끓이는 과정을 생각해 보자. 물이 담긴 주전자라는 계에 지금 외부에서 열이 공급되고 있다. 그 결과로 물과 주전자의 온도는 올라가고 이따금씩 주전자 뚜껑이 들썩거린다. 그러니까 외부에서 공급한 열량은 그 계가 일을 하거나 (주전자 뚜껑을 들어 올림) 내부의 에너지가 증가(물의 온도 증가)하는 데에 소요된다. 이것이 열역학 제1법칙이다. 에너지는 갑자기 생겨나거나 사라지지 않는다.

외부에서 가해진 열은 물을 끓이기도 하지만, 주전자 뚜껑을 들어올리기도 한다.
만약 빗면에 있는 구슬의 에너지를 높이려면 어떻게 해야 할까? 가장 손쉬운 방법은 구슬의 위치를 빗면을 따라 좀 더 올려주면 된다. 이렇게 되면 구슬의 퍼텐셜에너지가 커진다. 이때 우리는 구슬의 위치를 높이기 위해 중력을 거스르는 물리적 일(work)을 해 줘야만 한다. 우리가 구슬에 일을 해 준 그만큼의 에너지가 구슬의 퍼텐셜에너지로 저장된다.
스프링에 매달린 추에 대해서도 똑같은 이야기를 할 수 있다. 추의 탄성에너지를 높여주려면 우리는 스프링의 복원력을 거슬러서 ‘일’을 해 줘야만 한다. 외부에서 일을 해 준 양 만큼 추의 (혹은 스프링의) 탄성에너지로 저장된다. 에너지가 늘어나기 위해서는 외부에서 힘이 작용하여 일을 해 줘야만 한다.
질량을 포함한 새로운 에너지 보존 법칙을 제시한 아인슈타인
아인슈타인이 등장한 뒤에는 에너지 개념에도 혁명이 일어났다. 고전역학에서는 정지한 물체는 에너지를 가지지 않는다. 그러나 상대성이론에서는 정지한 물체가 그 질량에 비례하는 에너지를 가진다. 물리는 몰라도 누구나 다 아는 아인슈타인의 방정식이 있다.
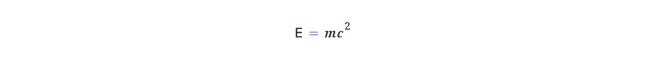
이 방정식은 질량이 에너지와 같다는 질량-에너지 등가의 관계를 말한다. 질량이 에너지와 관계가 있는 것은 아인슈타인의 4차원 시공간의 독특한 성질 때문이다. 여러분 손에 들려 있는 연필을 생각해 보자. 우리가 익숙한 3차원의 공간에서는 우리가 3차원의 좌표를 어떻게 잡더라도 연필의 길이가 변하지 않는다. 좌표를 어떻게 잡느냐에 따라 연필이 가리키는 방향은 마구 바뀌지만 그 길이는 변함이 없다. 아인슈타인은 시간과 공간이 결합된 4차원 시공간에서도 3차원에서의 연필의 길이와 마찬가지로, 4차원의 좌표가 임의로 바뀌더라도 변하지 않는 물리량이 있다고 생각했다.
그 중의 하나가 바로 정지질량이라는 양이다. 위치나 속도, 시간, 질량, 에너지 같은 양들은 좌표를 바꿈에 따라 항상 바뀐다. 하지만, 정지한 좌표계의 질량이나 시간은 어느 좌표계에서든 똑같은 값이다. 왜냐하면 변환된 좌표 자체에 살고 있는 사람은 자신의 좌표가 기준좌표이기 때문이다. 상대성이론에서는 상대적인 좌표가 중요하므로 모든 좌표계의 관측자 자신은 항상 정지해 있다. 그렇게 정지한 좌표계에서의 물체의 질량이나 시간은 항상 일정할 수밖에 없다. (물론 정지한 나의 좌표계에서 운동하는 상대방을 관찰하면 상대방의 물리량은 바뀐다.) 한편 상대성이론에서는 각 좌표들 사이의 상대속도가 중요하므로 질량과 속도를 조합한 물리량이 고전역학에서만큼이나 중요한 역할을 하리라 짐작할 수 있다. 고전역학에서는 질량을 속도와 결합해서 에너지(1/2 mv2)와 운동량(mv)을 만들 수 있다. (m은 질량, v는 속도) 아인슈타인은 에너지와 운동량을 잘 조합하여 4차원의 운동량을 도입했다.

핵분열에서 발생하는 에너지를 전기로 전환하는 핵발전소(프랑스)
이렇게 만들어진 4차원 운동량은 좌표를 변환하더라도 정지질량이 변하지 않는 방식으로 변환한다. 그렇게 되려면 에너지와 운동량이 정지질량을 매개로 하여 다음과 같이 독특하게 얽혀야만 한다.

여기서 p는 운동량이다. 물체가 정지해 있으면 (즉, p=0이면) 곧바로 E=mc2을 얻는다. 이 공식은 널리 알려진 대로 핵반응에서 어떻게 엄청난 에너지가 나오는지를 설명해준다.
우라늄이나 플루토늄을 중성자로 때려 연쇄 핵분열을 시키면 반응과정에서 생긴 질량 결손만큼 에너지로 방출된다. 그러나 핵분열 과정에서 감소하는 질량의 정도는 매우 작다. 만약 모든 질량이 에너지로 바뀔 수 있다면 실로 엄청난 양의 에너지를 얻을 수도 있을 것이다. 실제로 양자역학에서는 이런 일이 가능하다. 전자와 그 반입자(anti-particle)인 양전자(positron)가 충돌하면 빛이 되어 사라지는 반응이 정말로 일어난다. 이때는 전자와 양전자의 모든 질량이 빛의 에너지로 다 바뀐다. 전자-양전자뿐만 아니라 여타의 입자가 그 반입자와 만나면 이와 비슷한 반응이 일어난다. 하지만 현재 기술로는 실생활에 이용할 만큼의 에너지를 얻기 위한반물질을 생산하는 데에 또 다른 에너지와 시간이 너무 많이 소요된다.
에너지 보존 법칙에도 위기가 있었으나, 중성미자의 발견으로 해소되었다
에너지 보존 법칙은 언뜻 생각하면 무척 당연하고 또 꼭 그러해야만 할 것 같다. 하지만 한때 과학자들은 중성자가 붕괴하는 반응을 보면서 에너지 보존 법칙이 깨지는 게 아닌가라는 의구심을 가졌다. 중성자는 양성자와 전자로 붕괴한다. 이때 반응 전후의 에너지를 비교하면 원래 중성자가 가지고 있던 에너지가 붕괴 이후에 보존되지 않는 것처럼 보인다. 즉 양성자와 전자의 에너지를 더해도 원래 중성자의 에너지를 얻을 수 없었다.
이 문제를 해결한 사람은 볼프강 파울리(Wolfgang Pauli, 1900~1958)였다. 파울리는 전기적으로 중성이고 질량이 거의 없는 새로운 입자가 모자라는 에너지를 가지고 달아났을 것이라고 추정했다. 새 입자에는 중성미자(neutrino)라는 이름이 붙었다. 중성미자는 현대 물리학에서 가장 중요한 소립자 가운데 하나다. 이처럼 에너지 보존 법칙은 새로운 입자를 탐색하는 데에도 큰 역할을 한다.
우리 생활 주변에서 항상 함께 하는 에너지 보존 법칙

세계최초의 원자력 항공모함 USS Enterprise호. 승무원들이 갑판에서 아인슈타인의 공식을 만들면서 서 있다. <출처: US navy>
당연한 것 같은 에너지 보존 법칙의 원리를 잘 새겨두면 우리의 일상생활을 이해하는 데에도 큰 도움이 된다. 요즘 한창 논란이 되고 있는 전 지구적인 환경문제와 에너지 자원 문제를 생각해 보자. 지구라는 행성이 담고 있는 에너지 자원이 무한하지 않다. 또한 지구의 자연 환경에 절대적인 영향을 미치는 태양은 지구 표면의 1㎠ 당 매분 0.5cal의 열량을 공급한다. 만약 인간을 포함한 지구 생태계가 이 한계를 넘어서는 에너지를 소비하기 시작한다면 언젠가는 지구가 감당하기 어려운 상황에 직면할 것이다. 주어진 한계를 넘어서는, 끝없는 성장이란 불가능하다.
에너지 보존 법칙을 한마디로 정리하자면 “세상에 공짜는 없다.”는 말로 요약할 수 있다. 에너지는 어디서 느닷없이 생기거나 사라지지 않는다. 만약 전체 에너지를 높이고 싶으면 그 계에 일(work)을 해 주어야만 한다. 이런 면에서 에너지 보존 법칙은 다른 학문- 예를 들자면, 경제를 이해하는 데에도 쓸 만하다.
홈페이지 http://www.tenelux.com
'수학,과학,공학' 카테고리의 다른 글
| 738. 천체의 중력이 휘어 놓은 시공간 안에서 운동한 결과 (1) | 2022.10.13 |
|---|---|
| 737. 광속불변만 유지된다면 시공간쯤이야 (0) | 2022.10.13 |
| 726-불같은-사랑이-오래가지-못하는-이유 (0) | 2022.10.13 |
| 724. 자주 멍 때리기 (0) | 2022.10.13 |
| 723. eiㅠ+1=0 (0) | 2022.10.13 |