2022. 10. 15. 15:06ㆍ수학,과학,공학
코흐의 눈송이 곡선은 1.26차원
내 아이가 볼 만한
2018-01-29 13:23:17
1월 26일의 수학

코흐의 눈송이 곡선은 1.26차원
1904년 스웨덴의 수학자 헬게 폰 코흐(Koch)는 눈송이 모양을 닮은 흥미로운 곡선을 제안하였다. 처음에 한 변의 길이가 1인 정삼각형이 있다. 각 변을 삼등분한 다음 가운데 부분을 경사진 선 두 개로 교체한다. 이제 각 변은 네 개의 선분으로 대체되었고 각 선분의 길이는 1/3이다. 정삼각형은 12각형으로 바뀌었다. 다시 각 변을 삼등분 한 다음 가운데 부분을 경사진 선 두 개로 교체한다. 각 선분의 길이는 1/9로 줄어들고 12각형은 48각형으로 바뀐다. 이 과정을 계속 반복한다. 코흐의 눈송이 곡선은 이 과정의 극한으로 정의된다.
코흐의 눈송이 곡선은 꿈틀거림이 너무나 심하여 보통 우리가 알고 있는 곡선과 같은 종류의 것인지 의심이 든다. 코흐 곡선의 길이를 계산해보자. 1단계 12각형의 경우 곡선의 길이는
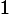






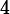
이다. 2단계 48각형의 경우 곡선의 길이는
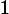



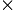

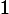






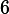


이다. 따라서

번째
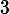



각형의 곡선의 길이는





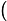





이다. 이 값은
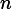
이 커짐에 따라 발산한다. 그렇다면 코흐 곡선의 길이는 무한대란 말인가? 무엇이 문제인가?

문제는 1차원 물체의 '길이'를 구하는 방식을 1차원이 아닌 물체에 적용한데 기인한다. 그렇다면 코흐 곡선은 몇 차원의 물체인가? 코흐 곡선에 대한 적절한 차원을

라고 하면 '길이'는














라고 정의해야 한다. 만약 넓이를 구한다면



가 적합한 값이고 부피를 구한다면



이 적합한 값일 것이다.

이 커져도 '길이'가 유한한

를 정하기 위해 로그를 취해 보면


















이 된다. 발산하지 않으려면















이 되어야 한다. 이 값이 바로 코흐 곡선의 적절한 차원이다. 보통 이 차원을 프랙털(fractal) 차원이라고 한다. 프랙털은 코흐 곡선과 같이 자기 유사성(self-similarity)을 가지는 물체를 부르기 위해 브누아 만델브로(Benoit Mandelbrot)가 만든 용어이다.
출처
제공처 정보
- 제공처
1946년에 설립된 대한수학회는 수학자들의 연구 및 교육 활동이 보다 원활하게 이루어지고 더 나은 환경을 구축하기 위해 지원하며, 수학공동체의 권익 증진과 학술적 가치를 기반으로 국내외 공익 기여를 통한 사회적 책무 수행을 위해 활동하고 있다. 또한 수학문화 확산 및 과학의 여러 부문과 협력하여 학술 문화 발전에 기여해 오고 있다.
매년 봄,가을 정기 연구발표회를 개최하며, 국내 수학 전문 학술지 중 유일하게 SCIE에 등재된 ‘대한수학회지(Journal of the KMS)’와 ‘대한수학회보(Bulletin of the KMS)’, 그리고 ESCI 등재지인 ‘대한수학회논문집(Communications of the KMS)’을 발행하고 있다.
'수학,과학,공학' 카테고리의 다른 글
| 1037. 케플러 법칙 (0) | 2022.10.20 |
|---|---|
| 1012. 고급유 논란의 종지부 (link) (0) | 2022.10.19 |
| 883. 왜 인간 눈에만 흰자위가 있나 -소통전략 (1) | 2022.10.15 |
| 881. ‘물체는 왜 추락할까’ 오랜 의문에 답하다. (0) | 2022.10.15 |
| 875. 불면증이 아닌 진화의 흔적 (0) | 2022.10.15 |
